Stefano Bussolon
Card Sorting, Category Validity, and Contextual Navigation
Abstract
One of the main goals of information architecture is to organize an informational domain into a usable taxonomy. This is, however, a difficult task: final users can classify the same domain differently from experts, differences can arise between different groups of users, and the same users can create different taxonomies for different goals (goal derived taxonomies).
Even using a participatory design - employing the card sorting technique - the resulting classification would be a sort of compromise, with some categories and items having a good consensus among users, and others being more problematic.
The aim of this paper is twofold. The first purpose is to propose some measure of the fitness of a taxonomy as a both whole and as individual items. Three measures will be presented: a) the consensus analysis; b) an index adapted from Tullis and Wood (2004), here called auto-correlation and c) a new measure, called category validity, conceptually similar to the cue validity introduced by Rosch and Mervis (1975). All of these measures can be calculated from the results of the card sorting.
The second goal is to present a contextual navigation that could ameliorate the findability of those items whose classification has been proven to be problematic, and to increase the information scent of the whole domain.
An example will illustrate the use of the category validity and the implementation of the contextual navigation.
Introduction
Humans can be defined as informavors, because they need information to survive and to accomplish their goals. In the digital age, an overwhelming amount of information is at our disposal at low costs or even for free. Ill structured, difficult to find information is, however, nearly useless. This is the reason why web search engines like Google have achieved such popularity. Search engines use mainly a brute force approach: a huge cloud of computers with sophisticated algorithms allows us to search any arbitrary keyword in a database of billions of documents in few milliseconds. This approach, though very useful, is however quite different from the way people searched and used information before the Internet age.
Humans structure their knowledge into semantic networks: sets of concepts (often verbally encoded) linked by different kind of relations. Usually the semantic networks are structured into some hierarchies that allow people to categorize their knowledge of their environment (Collins & Quillian 1996).
In the fields of classical artificial intelligence and knowledge engineering, the semantic networks are expressed by the use of the so called ontologies, whereas the hierarchical categories are defined by taxonomies. Though the term ontology brings with it the heritage of a very strong philosophical commitment (Guarino 1998), ontologies are usually defined in a more pragmatic way as a formal, explicit way to define entities, relations, rules and constraints (Uschold & Gruninger 1996; Noy & McGuinness 2001).
The design of meaningful, useful, flexible and coherent taxonomies and ontologies is one of the main goals of the information architecture, to provide to the users an effective way to find what they are seeking. Design for wayfinding is the first principle suggested by Wodtke (2002): “The goals of wayfinding are to let people know where they are, where the things they’re looking for are located, how to get to those things they seek”. In an interview with Marcos (2007), Peter Morville claims that “Findability is the major problem with most large web sites today, and information architecture is a big part of the solution.”.
In approaching this endeavor, an information architect can make use of different methodologies. There are fields of knowledge where well established taxonomies are olready at our disposal: the biblioteconomy is the best example of such a case. In other fields, powerful taxonomies have been developed by the scientific research. In all the other cases, however (and they represent the most frequent cases in the work of information architects) such a predefined taxonomy does not exist.
In those circumstances, the information architect needs the help of another person. Common sense suggests they should ask the experts, because they know the field of knowledge better than others and they should already have in mind a taxonomy, often very precise and detailed.
The user-centered design advice, however, is to focus our attention toward the end users (Maguire, 2001), and usually the users of the artifact we are designing are not the experts, but people whose level of expertise can be very different. The naive, implicit taxonomy of the end users can be significantly different from the one of the experts. This is one of the reasons why the involvement of the experts, though necessary, could be insufficient to develop a taxonomy that fits the needs of the users. A participatory approach can overcome this problem; methods like card sorting are used by information architects (Nielsen & Sano 1994; Rugg & McGeorge 1997; Coxon 1999; Maurer & Warfel 2004; Nielsen 2004; Fincher & Tenenberg 2005; Spencer 2009), social scientists (Ameel et al 2005) and psychotherapists (Upchurch et al 2001), to elicit the implicit knowledge of the users.
The aim of this paper is to emphasize the importance of a participatory approach in the definition of an information domain taxonomy, to propose different measures of the fitness of a taxonomy, and to propose an algorithm to provide a contextual navigation that could overcome some findability issues.
The next chapter is devoted to a short review of the cognitive theories of categorization and to some research work that underlines how different groups of people, with diverse goals, would generate dissimilar taxonomies. These findings will be used to justify the adoption of a participatory approach, and also to highlight how even the best taxonomy would not be free of problems.
When dealing with taxonomies, domain experts, final users and information architects would all recognize that some items are more difficult to classify than others, and that some solutions seem more satisfying than others. A measure of the goodness of a taxonomy could therefore help their work. In Chapter 2.2 three different indexes will be presented.
The consensus analysis is aimed to measure the concordance among participants and to verify the presence of significant differences among groups of subjects. The correlation between samples’ similarity matrices has been proposed by Tullis and Wood (2004) to measure “how many users are enough for a card sorting study” here, a variation of the method will be proposed that can give the practitioner a first suggestion to identify the more problematic items of a domain.
A third index, called category validity, will be proposed; its theoretical basis is rooted in the work of Rosch and Mervis (1975), and it will provide an index of the findability of every component of the classification.
In chapter 4, an algorithm will be proposed that could provide a contextual navigation and therefore increase the information scent of the system and the findability of the most difficult elements of a taxonomy. The category validity and the contextual navigation are both conceptually and practically related.
In chapter 5, an example will describe the use of the proposed measures and of the contextual navigation.
The Cognitive Theories of Categorization
The main cognitive theories of categorization will be briefly reviewed, as their claims would better justify the assumptions of this paper:
- The use of hierarchies as a natural and useful approach to organize an information domain;
- The utility of a participatory approach in the definition of such hierarchies;
- The utility, in the design of the navigation of the information space, to integrate the hierarchical navigation with a contextual navigation.
Assuming an evolutionary, ecological perspective, we can assume that people tend to categorize their environment for different reasons (Anderson 1991):
- Feature overlap. People notice that a number of objects share the same salient features, and proceed to form a category to include these items.
- Similar function. People notice that a number of objects serve similar functions and proceed to form a category to include them. It involves distinguishing between the functional and the non-functional features of an object.
- Linguistic labeling. Categories allow people to call different objects the same name.
These three views do not need to be in opposition. Rosch (1978) justifies the cognitive use of categorization citing two basic principles:
- Cognitive Economy. An organism has to maximize the information needed for his survival while minimizing the use of its cognitive resources.
- Perceived World Structure. The world is perceived not as an unstructured total set of equiprobable co-occurring attributes. Rather, the material objects of the world are perceived to possess a high correlational structure.
The early work of Collins and Quillian (1996) and the principles invoked by Anderson (1991) and Rosch (1978) cognitively justify the use of hierarchical structures to organize information. But why should we involve the users in defining them? Wouldn’t it be better to discover the ontologies and the taxonomies of the world represented and apply them to our information domain?
In the cognitive sciences, the formal taxonomies represent the logical outcome of the so called classical view of categorization (Smith & Medin 1981). In such a view, categories are assumed to be exact, not vague, to have clearly defined boundaries, and to have attributes in common which were the necessary and sufficient conditions for membership in the category. Furthermore, all members of a category must be equally valid with regard to membership (Rosch, 1999).
Those theories, however, have been questioned for a long time. A number of well-known experiments have demonstrated that the way humans categorize their world is significantly different [1]. What Rosch demonstrated is that categories are not exact, the boundaries can be (and usually are) blurred and overlapping, and the attributes are neither necessary nor sufficient (Lakoff 1987). In other words, the prototype theory confirms what information architects empirically find when they try to build a taxonomy.
Group Differences in Classification
Researchers have shown that different people can categorize the same set of items in different ways. Medin et al. (1997), for example, experimentally compared the way three different types of tree experts (e.g., taxonomists, landscape workers and parks maintenance personnel) categorized a list of tree species. The results showed an overall agreement, but also some significant differences among the three groups. Only the classification of the taxonomists correlated highly with the scientific taxonomy. Furthermore, the resulting clusters obtained by each group were different from the others.
Criteria of Classification
The differences found among the tree experts has been attributed not only to a different level of knowledge, but also to different criteria of classification. The research literature has been mainly focused on the study of single hierarchies, but in the real word there are many cases in which we have alternative organizations, the so called cross-classifications. In their work, Ross and Murphy (1999) asked their participants to generate some category names for each of 45 foods. Subjects were allowed 30 seconds for each food term and were asked to write down as many categories as they could think of. While 50% of the responses referred to the expected taxonomic categories, 42% of the generated categories referred to the situation in which the food was eaten, such as breakfast foods or snacks, or to the healthiness of the foods, such as healthy or junk foods.
The authors called them script categories, because they usually indicate a time or situation in which the food is eaten.
These results suggest that people may have alternative organizations or cross-classifications. They demonstrate the existence of categories based on interactions with the objects rather than on their taxonomy. Such an organization may be especially helpful in generating plans and in decision making.
Murphy (2001) studied a similar issue: the distinction between taxonomic and thematic classification. Thematic classifications are defined as those relationships in which things are grouped together because they occur within the same setting or event, or because one of them fulfills a function of the other one. Murphy arranged a set of nine stimuli that could be grouped both using a taxonomic and a thematic criterion, and found that his subjects (undergraduate students) used the thematic criterion more often than the taxonomic.
Goal-derived Categories
It is usually assumed that taxonomies are stable in people’s minds. In contrast, the concept of goal-derived categories offers a perspective in which the individual actively constructs cognitive representations to achieve salient goals (Barsalou, 1983; Ratneshwar et al., 2001). The results of the work of Ratneshwar et al. (2001), for example, suggest that personal and situational goals can exert a systematic impact on category representations. People with different goals would classify the same domain in different ways.
When the Best Solution is not Enough
The experimental evidence reported here justifies the first two assumptions that have been made: people naturally organize their knowledge into taxonomies, and non-experts tend to classify information domains in ways that are systematically different from experts’ taxonomies. We therefore need to involve the final users to discover the structure that better fits with their mental representation and their goals.
The best solution, however, is generally a sort of compromise that combines the opinion of experts and the cluster analysis of card sorting. Such a solution can be very effective and free from problems, when the consensus among such different stakeholders is high. What the cited research and our practical experience tells us, however, is that in the real word something different happens: the resulting taxonomy results in some branches where the consensus is very high, while in other parts the consensus is lower. Usually some items emerge whose classification proves to be problematic. In those circumstances the assignation of an item to one of two or three categories becomes an arbitrary, though reasonable, decision.
Measuring Fitness
Miller et al. (2007) provide an empirical support of this claim. In their work they asked 15 participants to classify a number of items using a closed card sorting. They assumed that the category with the most selections had to be considered the “correct category”, and calculated that, on average, participants selected the correct category 6.6% of the time, producing an error rate of 30.4%.
The problem with these kinds of items is their findability: the lower the consensus among users on where to put them, the higher the probability that they would seek them in the wrong cluster. A solution proposed by Miller et al.(2007), could be represented by inserting those items into more than one category; this is, however, a violation of the constraints of the taxonomies. Furthermore, it could lead to some confusion in the mental model of the users.
Consensus Analysis
Consensus analysis is a method developed to obtain quantitative estimates of the similarities and differences in the structures of semantic domains in different groups (Romney et al 1986; Gatewood 1999; Boster 2001).
The first goal of consensus analysis is to estimate the level of knowledge of each informant where the domain is not known in advance by the researcher, but it can also be used to see if the participants belong to a homogeneous culture, or if two or more subcultures emerge from the questionnaire.
Consensus analysis provides a measure of the degree of agreement among participants. Its calculation is based on the principal component analysis of the matrix of the participants. If the ratio between the first and second principal component is greater than 3:1, we can say that there is a single factor solution, or a “cultural” level of agreement. The 3:1 ratio is a widely adopted convention for consensus analysis (Caulkins et al., 2000).
Consensus analysis can be applied to the results of card sorting to measure the homogeneity of the classifications, the presence of clusters of subcultures, and to estimate the reliability of the answer of each participant. This method can help the information architect to identify the most representative participants and to evaluate the opportunity to design different taxonomies for the subgroups identified. The application of the consensus analysis to the card sorting data has been described in Bussolon (2008).
Correlation between Samples Similarity Matrices
Tullis and Wood (2004) were interested in measuring “how many users are enough for a card sorting study,” and they proposed to use as an index the correlation between the similarity matrices of two samples of participants.
The following algorithm can be used to measure the reliability of the results of a card sorting: the participants can be randomly divided into two groups of equal size; for each group the proximity matrix is generated, and the correlation between the two matrices is computed.
The same algorithm can be adapted to measure the reliability of each item. Each item corresponds to a row (and a column) in the matrix. If we calculate the correlation of the corresponding rows of the two matrices, we can obtain an index for each of the items. This measure can be called the autocorrelation of the item. The lower the auto-correlation of an item, the lower the consensus among participants. The inverse, however, is not always true because it is possible that a problematic item would have a high autocorrelation.
An example can help to explain this occurrence. Let’s imagine a card sorting with 100 participants in which 50 people put a certain item into category A, whereas the other 50 put the same item into category B. If we split the participants into two random groups, it is probable that in both matrices 25 people assigned the item to group A and 25 to group B. The correlation would therefore be high, even if the consensus is low.
In any case, this method can be very useful in describing the difficulty and the complexity of a card sorting task: some lists of elements are easier to classify, whereas others are far more difficult. A second variable is the different level of expertise and motivation of the participants. It is therefore a good practice to determine in advance a correlation threshold, and recruit as many participants as necessary to reach that threshold.
Cue Validity and Category Validity
In formalizing the concept of Family Resemblance introduced by Wittgenstein (1953), Rosch and Mervis (1975) introduced the concept of cue validity, which is defined in terms of the frequency of a cue (a feature) within a category and its proportional frequency in that category relative to contrasting categories.
In their experiments, Rosch and Mervis (1975) showed that the cue validity of each item correlates with its typicality.
We can assume that there is a positive correlation between the typicality of an element and its findability. A measure of the typicality of an element inside a category would, therefore, constitute a good measure of its findability. The most obvious way to measure the typicality of an element is to ask the users to rate it. This measure is indeed very reliable, but this approach implies that a new questionnaire must be given. Nor can we calculate the cue validity of the items, because this implies that we know their attributes, information which is not available with card sorting.
We can, however, calculate an index that is conceptually similar to cue validity. Mathematically, cue validity is the frequency with which a cue is associated with the category in question, divided by the total frequency of that cue over all relevant categories. The measure proposed here is mathematically similar.
The proximity matrix is a square, m*m matrix, where m represents the number of items. Each cell ci;j represents the number of times that the item i and the item j have been categorized into the same group.
Given a partition of the elements (calculated, for instance, with the k-means algorithm), we can calculate for each element the category validity using the following formula:
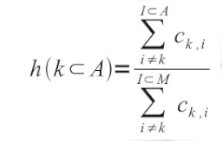
where h (k) is the Category Validity of the item k, I⊂A are the elements who belongs tho the same A category of k (except k itself) and I⊂M are all the elements (except, again, k).
The algorithm, therefore, sums all the cells of a given k row (except the diagonal value c(k,k) ), all the cells of the elements who belongs to the same category of k (except, again, the diagonal value c(k,k)), then divides the latter value with the former. The formula reaches it’s maximum value (1.0) when an element has been categorized, by all the participants, with the items of it’s category, and never with the other items.
An example can help to better explain the calculation. Let’s take the following proximity matrix:
| Item 1 | Item 2 | Item 3 | Item 4 | Item 5 | Item 6 | Item 7 | |
|---|---|---|---|---|---|---|---|
| Item 1 | 100 | 88 | 88 | 64 | 8 | 4 | 0 |
| Item 2 | 88 | 100 | 82 | 62 | 16 | 14 | 12 |
| Item 3 | 88 | 82 | 100 | 54 | 18 | 14 | 12 |
| Item 4 | 64 | 62 | 54 | 100 | 42 | 36 | 36 |
| Item 5 | 8 | 16 | 18 | 42 | 100 | 88 | 2 |
| Item 6 | 4 | 14 | 14 | 36 | 88 | 100 | 6 |
| Item 7 | 0 | 12 | 12 | 36 | 2 | 6 | 100 |
Items 1, 2, 3 and 4 are clustered into group A; items 5, 6 and 7 into group B. To calculate the category validity for item 1 we have to calculate
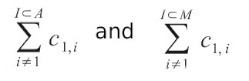
The first formula sums the cells c(1,2), c(1,3) and c(1,4) (items 2, 3 and 4 belongs to the same group A of item 1). The second formula sums all the cells of the first column but the first (c(1,1)). The result of the first sum is 88 + 88 + 64 = 240. The result of the second sum is 88 + 88 + 64 + 8 + 4 + 0 = 252. The category validity of item 1 is therefore 240 / 252 = 0.52.
To calculate the category validity for item 4 we have to calculate

The first formula sums the cells c(4,1), c(4,2) and c(4,3) (items 1, 2 and 3 belongs to the same group A of item 4). The second formula sums all the cells of the 4th column but not c(4,4). The result of the first sum is 64 + 62 + 54 = 180. The result of the second sum is 64 + 62 + 54 + 42 + 36 + 36 = 24. The category validity of item 4 is therefore 180 / 24 = 0.612. Correlation between
Correlation between Measures
In the previous paragraphs some assumptions have been made. The first is that both the auto-correlation and the category validity should measure the findability of an element. If this is true, a correlation between the two measures should be found. The second assumption is that there is a correlation between the typicality of an element and its category validity. In a correlational research (Bussolon et al 2005) we measured the correlation between typicality, free listing frequency, semantic decision task and the correct answers of a closed card sorting. We asked participants to produce, rate and categorize a list of animals into the categories mammals, fish, reptiles and birds, and then calculated the correlation between those measures [2].
To verify the correctness of the assumptions made, the same dataset has been used to calculate the correlations between measures. Figure 1 shows the dispersion graph of the correlations calculated.
Category Validity
The Pearson correlation between the auto-correlation and the typicality rate is r(S) (df = 53) = 0.407, p = 0.002 (graphic top-right of fig. 1).
The Pearson correlation between the auto-correlation and the number of correct classification in the card sorting is r(S)(df = 53) = 0.682, p < 0.001 (graphic middle-right of fig. 1).
The Pearson correlation between the auto-correlation and the free listing production rate is r(S)(df = 53) = 0.1, p = 0.16.
The Pearson correlation between the auto-correlation and the mean correct responses in the semantic decision task is r(S)(df = 53) = 0.684, p < 0.001 (graphic bottom-right of Figure 1).
The Pearson correlation between the auto-correlation and the mean reaction times in the semantic decision task is r(S)(df = 53) = -0.55, p < 0.001.
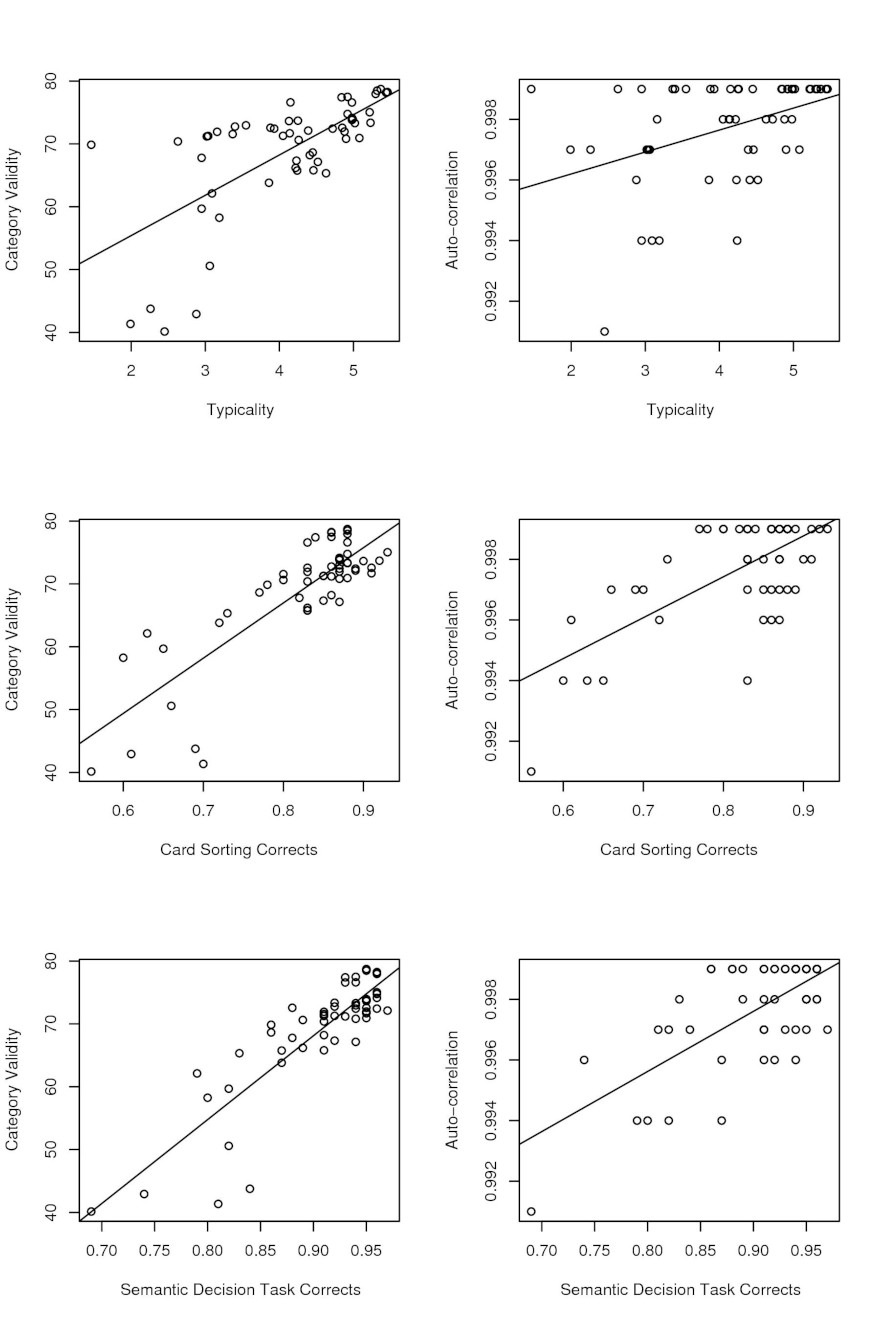
Figure 1. Correlations between the different measures
On the left of Figure 1, the category validity and its correlation with the typicality rate (top), card sorting correct answers (middle) and semantic decision task correct answers (bottom). On the right, the correlation between the auto-correlation and typicality rate, card sorting correct rate and semantic decision task correct answers.
Category Validity and Auto-correlation
Finally, the correlation between category validity and auto-correlation has been calculated. For the list of animals, the Pearson correlation is r(S)(df = 53) = 0.677,p =< 0.001. The same index has been calculated for the other research datasets our research group collected in recent years:
- a list of gifts in an imaginary e-commerce site: correlation = 0.72;
- a list of worldwide tourist locations for an imaginary on-line tour operator [3]: correlation = 0,60p < 0.001;
- a list of positive and negative emotions; correlation = 0,46p < 0.001.
Conclusions
From a theoretical, cognitive perspective, the most important measure is the correlation with the typicality rate. Both measures proposed here significantly correlate with it: 0.68 for the category validity, 0.40 for the auto-correlation. These results validate the second assumption made: the category validity can be assumed to be a reliable indicator of the typicality of an element. For a practical perspective, the correlation with the correct responses in the closed card sorting and in the semantic decision task assumes a particular importance: the items with a lower category validity are those with the higher error rate.
CONTEXTUAL NAVIGATION
The correlational studies presented in the previous chapter confirm the validity of the proposed index as a measure of the findability of the elements of a taxonomy. The category validity (and, in a lesser measure, the autocorrelation) can be used as a diagnosis tool by the information architect. It can tell her when she can trust the card sorting results and where difficulties arise. The voices with a low category validity are, probably, where the practitioner should focus her attention. It does not, however, provide a cure for the problem.
A possible solution can be found using contextual navigation. The taxonomy of an information system represents for the information architect one dimension of what Norman (1988) defines as the design model. In Norman’s model, the user can create his own mental model through what he calls the system image. In a hypertext environment, the system image of the taxonomy is provided by the navigation system. Garrett (2003) maintains that the navigation design must accomplish three goals: to provide users with a means for getting from one point to another, to communicate the relationship between the elements it contains and to communicate the relationship between its contents and the page the user is currently viewing. Multiple snavigation system are usually provided to accomplish those goals.
With a strong emphasis on hierarchical taxonomy, Park and Kim (2000) distinguish between up-to-parent, down-to-child, next-to-peer, up-tograndparent and down-to-grandchild links. Garrett (2003) defines global navigation as links to the home page and to the main categories of the taxonomy; local navigation provides access to the parent, the siblings and the children elements; supplementary navigation provides shortcuts to related content not directly accessible by the taxonomy; contextual navigation corresponds to in-line navigation; and courtesy navigation links to convenience pages like contact information and policy statements. Wodtke (2002) calls navigation to siblings crabwalking.
Rosenfeld and Morville (2007) distinguish between global, local and contextual navigation and between hierarchical and lateral navigation. Lateral hyperlinks “allow users to move laterally into other branches” (Rosenfeld and Morville, 2007, Page.121). Their definition of contextual navigation emphasizes the creation of links specific to a particular page, document or object. They cite the “See Also” links to related products in e-commerce sites. A famous, and very useful, example of contextual navigation is used by Amazon: “Customers Who Bought This Item Also Bought”.
A smart use of contextual, supplementary navigation could be a solution to improve the findability of the items with a low category validity. Using a “See Also” list of links, the designer can show the ambiguous items in all the category pages where the user could search for them.
The contextual navigation can be designed by hand, but the data from the card sorting can help by giving us some smart suggestions.
Automatic Contextual Navigation
An algorithm that uses the proximity matrix of the card sorting can be used to generate the contextual navigation. The reader should remember that the proximity matrix is a square, m*m matrix, where m is the number of elements, and that in every cell ci;j is coded the number of times that the items i and j have been categorized together.
Similarly, with the category validity algorithm, the first step is to extract the row of the matrix corresponding to the element for which the contextual navigation has to been generated.
The second step is to sort the vector in a decreasing order. The result is the list of all the elements, ordered by the number of times they have been classified together with the target item. This is the basis of the contextual navigation. Usually, the voices in the same category of the target element (the siblings) are already listed in the local navigation. If this is the case, those elements should be deleted from the ordered list. The first remaining elements of the list are the candidates for the contextual navigation. The designer can decide to include a fixed number of items (for example, the first 5).
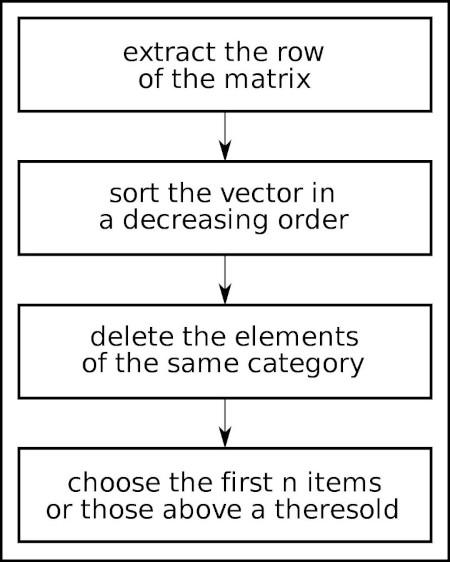
Figure 2. The diagram of the algorithm for the automatic contextual navigation
A different solution is to identify a cut-off, including all those voices that have been classified together a number of times greater than the cut-off.
An example
We can use the matrix of the example on page 13 to explain the algorithm proposed. We can decide to include in the contextual navigation those items that have been classified together with the target item at least the 30% of the times. To calculate the contextual navigation of the first item, we select the corresponding row (column c1;1 has been omitted).
| Item 2 | Item 3 | Item 4 | Item 5 | Item 6 | Item 7 |
|---|---|---|---|---|---|
| 88 | 88 | 64 | 8 | 4 | 0 |
The second step is to sort the vector. In this example it is already sorted. The third step is to delete the items that belong to the same group of item 1: items 2, 3 and 4. The first candidate for the contextual navigation is therefore item 5. However, items 1 and 5 have been classified together only eight percent of the time, so therefore we would decide to let the contextual navigation empty. For item 4, the row is
| Item 1 | Item 2 | Item 3 | Item 5 | Item 6 | Item 7 |
|---|---|---|---|---|---|
| 64 | 62 | 54 | 42 | 36 | 36 |
Once again, the vector is already sorted. We delete items 1, 2 and 3 because they belong to the same group. Items 5, 6 and 7 have all been classified with item 4 more than the 30% of the time, which is the amount we chose as our cutoff, and therefore they will all appear on the contextual navigation.
What can be noted is that the contextual navigation is more important for those items whose category validity is lower. Item 1 is strongly linked only with the items in the same group, and therefore the category validity is high and the contextual navigation is unnecessary. Item 4 has significant links with items 5, 6 and 7 outside its group. Those links causes the low category validity and thus the need for the contextual navigation.
Text categorization
A different approach to creating a taxonomy and identifying a contextual navigation is represented by research in the field of text categorization, where a wide range of statistical and machine learning techniques are used to automatically classify a corpus of textual documents (Dumais and Chen, 2000).
The main advantage of the solution we propose is that it is based on a participatory, user-centered design that allows the emergence of latent classification criteria and items relationships that are not always coded in the documents do be classified. A second advantage is that it does not require the existence or the availability of a textual corpus which can be absent when a completely new website, or a new section of an existing web site, is designed. The main disadvantage, of course, is that it requires the results of a card sorting.
The two approaches, however, can be combined, both to design the taxonomy and to generate the contextual navigation.
A CASE STUDY
An example can help to explain both the measures proposed in the previous chapter and the automatic contextual navigation algorithm. The aforementioned list of tourist destinations were used as a dataset. It consisted of a list of places (cities, regions or states) people would like to visit. The list was generated from an on-line free listing task. The locations most often cited by the participants were selected and used for an open card sorting task. This dataset was chosen because even if the names of the places are in Italian, most of then were still understood by English readers.
The Free Listing
A free listing questionnaire was used to collect a list of places. The participants were recruited on-line, through an invitation to participate in an on-line questionnaire which appeared on a couple of web sites. Subjects were asked to list up to ten places they would like to travel for a vacation: “Where would you like to go for a vacation? List up to ten places where you would like to spend your vacations.” The questionnaire was given in Italian. 25 participants took part in the test. Of them, 15 completed it: 73 male, 120 female; 2 people did not declare their gender. 186 participants declared their age. Mean age was 33 years. 785 distinct responses have been produced. The most frequent answers were: parigi [francia] (85); roma (lazio) (53); londra [inghilterra] (41); barcellona [spagna] (38); firenze (toscana) (34); madrid [spagna] (30); sidney [australia] (28); venezia (veneto) (28); amsterdam [olanda] (23); new york [stati uniti] (20); mosca [russia] (1); new york [usa] (1); palermo (sicilia) (18); napoli (campania) (17); atene [grecia] (15); lisbona [portogallo] (15); vienna [austria] (15); berlino [germania] (14); pechino [cina] (13); dublino [irlanda] (12).
The Card Sorting
An on-line card sorting questionnaire was given with the names of the places obtained by the free listing. 82 places were used as the items to be classified. The participants were asked to classify the places. The questionnaire was held in Italian. The instructions were: “Imagine you have to design the web site of a travel agency, and your aim is to show the touristic destinations in a coherent taxonomy: how would you group those places?” Users were given the list of places and six empty lists. Using some buttons, the subjects were required to group the items into coherent groups.
An on-line card sorting questionnaire was given with the names of the places obtained by the free listing. 82 places were used as the items to be classified. The participants were asked to classify the places. The questionnaire was held in Italian. The instructions were: “Imagine you have to design the web site of a travel agency, and your aim is to show the touristic destinations in a coherent taxonomy: how would you group those places?” Users were given the list of places and six empty lists. Using some buttons, the subjects were required to group the items into coherent groups.
4100 participants took part in the test. Of them, 608 completed it: 24 male, 351 female; 8 people did not declare their gender. 582 declared their age with a mean age of 33 years. Education level not declared: 12; primary school (8 years): 70; secondary school (13 years):22; bachelor degree (16 years): 63; Master degree (18 years): 171.
Statistical analysis
The first step was to calculate the proximity matrix. Using the proximity matrix, a dendrogram was calculated, using a hierarchical cluster analysis (Berkhin, 2007) [4]. Figure 3 represents the resulting dendrogram.
K-means is a different clustering algorithm that can be used to generate a partition from a set of elements (Berkhin, 2007; Xu and Wunsch, 2005). Ding and He (2004) suggest calculating a principal component analysis before calculating the k-means; Principal Components Analysis (PCA) is an exploratory multivariate statistical technique for simplifying complex data sets (Raychaudhuri et al., 2000), and the first eigenvectors can be used to map the elements on the principal components’ space.
Following Ding and He (2004), a k-means analysis can be calculated using the first k-1 dimensions of the PCA. Figure 4 is the result of a k-means clusterization: the position of the items on the x and y axes corresponds to their loadings on the first and second components of the PCA, and the different colors represent the different categories.
The most recognized limit of the k-means algorithm is that the resulting partition depends strongly on the initial random assignment of centroids (Berkhin, 2007).
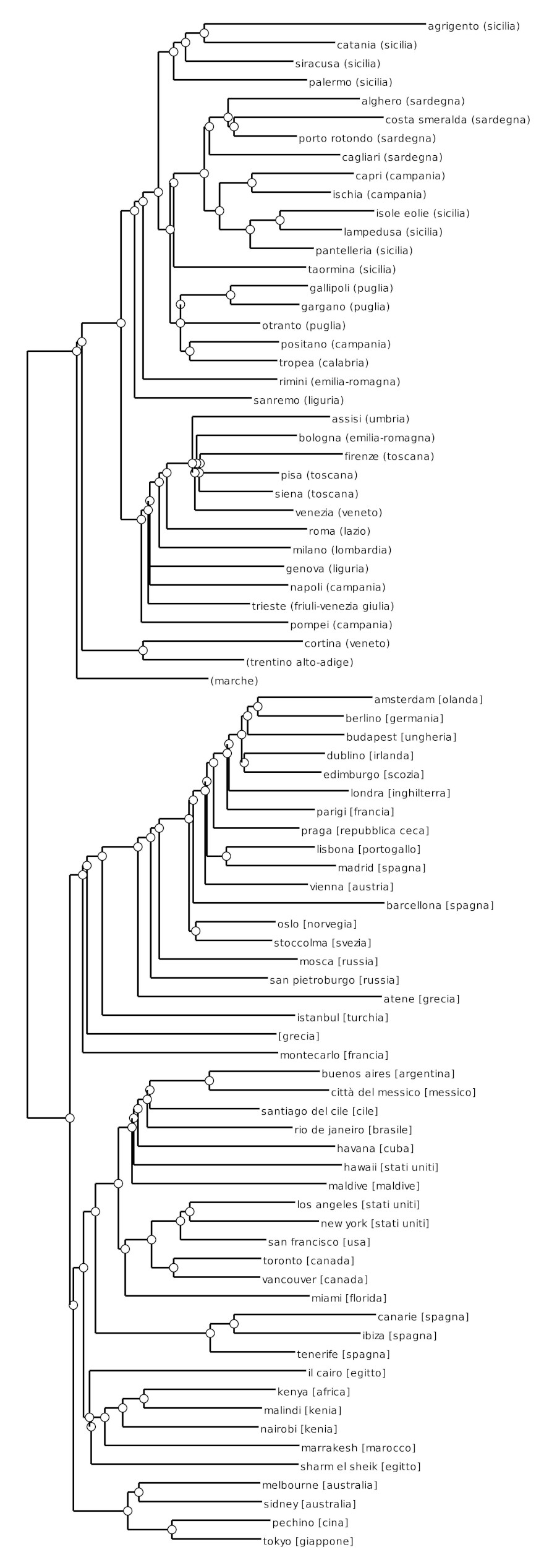
Figure 3. The dendrogram of the hierarchical cluster analysis.
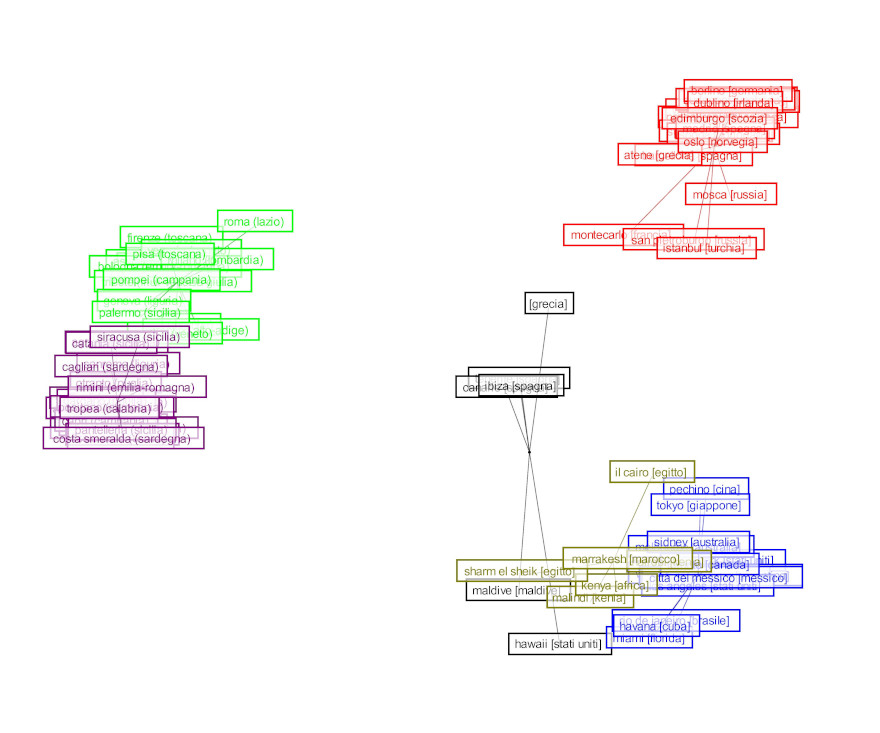
Figure 4. The results of the k-means
In Figure 4, The items are placed on the x and y axes based on their loadings of the first and second principal component analysis. The colors represent the clusters.
Since both the computation of the category validity and the construction of the final taxonomy are based on the results of the k-means, a further step has been made to minimize the impact of the non-deterministic aspects of the kmeans: 100 different k-means partitions have been generated; for each partition and for each element, the corresponding category validity has been calculated. The final category validity index is, therefore, the average of the results of the 100 partitions. To generate the taxonomy, the partition with the lower sum of distances between the items and their centroids has been chosen.
Figure 5 represents the sitemap generated by the results of the Card Sorting.
Finally, the auto-correlation of the items and the consensus analysis of the participants have been calculated.
Results
Category Validity: The elements with higher category validity are Berlin, Dublin, Budapest, Amsterdam and London. The items with lower validity are Greece, Hawaiian Islands, Cairo, Ibiza and Tenerife.

Figure 5. The sitemap generated by the results of the card sorting
Interestingly, the elements with greater category validity are the ones more polarized on both the first and second principal component, while the ones with lower validity lie in the middle of the space. This result is compatible with the results of Lynch et al. (2000).
The algorithm to calculate the category validity can be shown through two examples: Berlin (a high validity item) and the Hawaiian Islands (a low validity item). Berlin is classified among the “European cities” (“città europee”) cluster. The corresponding row in the proximity matrix is selected, and the vector is ordered. The first 18 elements of the list are the 18 other places in the same category: Amsterdam (525), Budapest (512), Dublin (504), London (488) and so on. To calculate the category validity, first the sum of the values for all the items is calculated, followed by the sum of the values of the 18 elements within the same category. The category validity is the second result divided by the first. Hawaii is placed within the “mare estero” category (seaside abroad Italy). Looking at the ordered vector, however, one can note that the five elements of the same category are not all at the top of the list. The first element, Havana (363), belongs to a different category. Maldive (361) is second, Ibiza (273) fourth, Canary (268) fifth, Tenerife (227) tenth and Greece (123) in 27th place. This is the main reason for the low score on the category validity for Hawaii.
Auto-correlation and consensus analysis: The correlation between category validity and auto-correlation is = 0, 60p < 0.001. The elements with the lower auto-correlation are Ibiza, Canary Islands, Greece, Tenerife and Cairo.
The consensus among participants is very high. The ratio between the first and the second component is 7.3.
Contextual navigation
Figure 6 shows the navigation of six different cities: Barcelona, Paris, Cairo, Sharm el Sheik, Canary Islands and Hawaiian islands. Barcelona and Paris are clustered as “European cities” (“città europee”), Cairo and Sharm el Sheik as “Africa”, and the Canary Islands and Hawaiian islands as “seaside abroad” (mare estero). The local navigation of each pair of places is the same. What changes is the contextual navigation (labeled “Related items”). The page for Barcelona, for example, suggests three Spanish places (clustered amongst “Seaside abroad”), whereas the page for Paris suggests, among others, cities like Beijing, Rome and New York.
The page of Sharm el Sheik, a seaside place, suggests other seaside places like the Maldive islands, Tenerife, the Canary Islands, Ibiza, Hawaii and Miami. Cairo, the other Egyptian location on the list, though being clustered in the same category, suggests cities like Istanbul, Athens, Mexico City, Buenos Aires, Beijing, and Santiago del Chile.

Figure 6. Some examples of local and contextual navigation: a) Barcelona, b) Paris, c) El Cairo, d) Sharm el Sheik, e) Canaria islands, f) Hawaii islands
Conclusions
Solid experimental evidence supports the assumption that taxonomies are a good and cognitively natural way to structure the data within an information system. Different people, however, categorize the same data in different manners; a participatory approach is therefore the best way to elicit the implicit taxonomies of the users of an information domain. The final architecture that emerges from a participatory design of an information system is usually a compromise between the stakeholders’ needs and the diverse users’ expectations. The best efforts of the information architect, however, do not guarantee a satisfactory level of findability for all the elements of the domain.
If a card sorting questionnaire is used as a base for the taxonomy, some indexes can be calculated to measure its fitness. The consensus analysis, the auto-correlation index and the category validity have been described. The category validity has been shown to be a reliable measure of the difficulty of finding an item.
A contextual navigation has been proposed that should improve the findability of the difficult elements, without violating the hierarchical structure of the system. In designing the contextual navigation of the items, an algorithm that uses the proximity matrix of the card sorting can suggest the best candidates to list. This supplementary navigation should not only increase the findability of the elements, but also the information scent of the pages (Chi et al., 2000) and the contextual information that helps the users to understand where they are and where they can go (Park and Kim, 2000).
Limitations of the Study
The category validity measure has been proven to correlate positively with the typicality, and negatively with error rates in the card sorting task and in a semantic decision task in a domain where the correct answers were known by the researchers. This result supports the assumption that the category validity is a good measure of the findability of an element. More direct experimental evidence would be necessary, however. The same can be stated for the contextual navigation proposed in chapter 4; the qualitative analysis of the empirical results shown in chapter 5 seems to confirm the utility of the contextual navigation but, again, experimental evidence would provide much stronger support to the proposal.
The category validity algorithm has the advantage of being very simple. In the present form, however, it is probably biased by the number of elements within a category: the elements belonging to the smallest categories tend to have a lower validity. This bias could be corrected by including the size of the category into the denominator of the formula.
A limitation of the contextual navigation presented here is that - in the present form - it can be implemented only at the level of the leaf elements, but not at the level of the categories; the user has to choose an element before the navigation would suggest to her the related items. Such a suggestion would be very useful when the user adopts a serendipitous navigation style, but if she is looking for a particular element by choosing a similar but incorrect element and hoping that the contextual navigation will suggest to her the right one, this is not the best example of usability. A contextual navigation system able to suggest related elements at the category level would dramatically increase the usefulness and usability of the navigation system.
References
- Ameel, E., Storms, G., Malt, B. C., and Sloman, S. A. (2005). How bilinguals solve the naming problem. Journal of Memory and Language, 52:30-32.
- Anderson, J. R. (1991). The adaptive nature of human categorization. Psychological Review, 8(3):40-42.
- Ashby, F. G. and Maddox, W. T. (2005). Human category learning. Annu. Rev. Psychol., 56:14-178.
- Barsalou, L. W. (1983). Ad hoc categories. Memory and Cognition, 11(3):211-227.
- Berkhin, P. (2007). Survey of clustering data mining techniques. [On-line; accessed 2-August-2007].
- Boster, J. S. (2001). The information economy model applied to biological similarity judgment, pages 203-225.
- Bussolon, S. (2008). Cultivating diversity in information architecture: the consensus analysis. In UPA Europe. UPA Europe.
- Bussolon, S., Ferron, M., and Del Missier, F. (2005). On-line categorization and card sorting. In Cognitive processes in ergonomy and human computer interaction. Alps-Adria conference in psychology, Zadar, (Croazia).
- Caulkins, D. D., Trosset, C., Painter, A., and Good, M. (2000). Using scenarios to construct models of identity in multiethnic settings. Field Methods, 12(4):267-281.
- Chi, E., Pirolli, P., and Pitkow, J. (2000). The scent of a site: A system for analyzing and predicting information scent, usage, and usability of a web site. In CHI Letters, volume 2. CHI.
- Collins, A. M. and Quillian, R. M. (1996). Retrieval time from semantic memory. Journal of Verbal Learning and Verbal Behavior, 8:240-247.
- Coxon, A. P. M. (1999). Sorting data. Sage Publications. Collection and analysis.
- Ding, C. and He, X. (2004). K-means clustering via principal component analysis. In 21st International Conference on Machine Learning.
- Dumais, S. and Chen, H. (2000). Hierarchical classification of web content. In Proceedings of the 23rd annual international ACM SIGIR conference on Research and development in information retrieval, pages 256-263.
- Faiks, A. and Hyland, N. (2000). Gaining user insight: a case study illustrating the card sort technique. College and Research Libraries, pages 34-357.
- Fincher, S. and Tenenberg, J. (2005). Making sense of card sorting data. Expert Systems, 22(3):8-3.
- Garrett, J. J. (2003). The elements of user experience. New Riders, Berkeley - CA - US.
- Gatewood, J. B. (1999). Culture ... one step at a time. The Behavioral Measurement Letter.
- Guarino, N. (1998). Formal ontology and information systems. In Guarino, N. (ed) Formal Ontology in Information Systems. Proceedings of FOIS ’8, pages 3-15. IOS Press - Amsterdam.
- Lakoff, G. (1987). Women, fire, and dangerous things. The University of Chicago Press, Chicago.
- Lynch, E. B., Coley, J. D., and Medin, D. L. (2000). Tall is typical: Central tendency, ideal dimensions, and graded category structure among tree experts and novices. Memory and Cognition, 28:41-50.
- Maguire, M. (2001). Methods to support human-centered design. Int. J. Human-Computer Studies, 55:587-634.
- Marcos, M.-C. (2007). Information architecture and findability: Peter Morville interview. El profesional de la informacion, 16(3):268-26.
- Maurer, D. and Warfel, T. (2004). Card sorting: a definitive guide. Technical report, World Wide Web.
- Medin, D. L., Lynch, E. B., and Coley, J. D. (1997). Categorization and reasoning among tree experts: Do all roads lead to rome? Cognitive Psychology, 32:4-6.
- Miller, C. S., Fuchs, S., Anantharaman, N. S., and Kulkarni, P. (2007). Evaluating category membership for information architecture. Sig CHI.
- Murphy, G. L. (2001). Causes of taxonomic sorting by adults: A test of the thematic-to-taxonomic shift. Psychonomic Bulletin & Review, 8(4):834-83.
- Nielsen, J. (2004). Card sorting: How many users to test. html page, World Wide Web.
- Nielsen, J. and Sano, D. (1994). Sunweb: User interface design for sun microsystem’s internal web. In Proceedings of the 2nd World Wide Web Conference ’4: Mosaic and the Web, pp. 547-557, http://www.internettg.org/newsletter/dec/cluster_analysis.html.
- Norman, D. A. (1988). The psychology of everyday things. Basic Books.
- Noy, N. F. and McGuinness, D. L. (2001). Ontology development 101: A guide to creating your first ontology. Technical report, Stanford University, Stanford, CA.
- Park, J. and Kim, J. (2000). Contextual navigation aids for two world wide web systems. International Journal of Human-Computer Interaction, 12(2):13-217.
- Ratneshwar, S., Barsalou, L. W., Pechmann, C., and Moore, M. (2001). Goalderived categories: The role of personal and situational goals in category representations. Journal of Consumer Psychology, 10(3):147-157.
- Raychaudhuri, S., Stuart, J. M., and Altman, R. B. (2000). Principal components analysis to summarize microarray experiments: application to sporulation time series. Pacifc Symposium on Biocomputing, 5:452-463.
- Romney, A. K., Weller, S. C., and Batchelder, W. H. (1986). Culture as consensus: A theory of culture and informant accuracy. American Anthropologist, 88(2):313-338.
- Rosch, E. (1978). Cognition and Categorization, chapter Principles of Categorization. Hillsdale NJ, LEA.
- Rosch, E. (1999). Reclaiming concepts. The Journal of Consciousness Studies, 6(11-12):61-77.
- Rosch, E. and Mervis, C. B. (1975). Family resemblances: Studies in the internal structure of categories. Cognitive Psychology, 7(4):573-605.
- Rosenfeld, L. and Morville, P. (2007). Information architecture for the World Wide Web. O’Reilly and Associates, Inc., Sebastopol, CA, USA, 3rd edition.
- Ross, B. H. and Murphy, G. L. (1999). Food for thought: Cross-classification and category organization in a complex real-world domain. Cognitive Psychology, 38:45-553.
- Rugg, G. and McGeorge, P. (1997). The sorting techniques: a tutorial paper on card sorts, picture sorts and item sorts. Expert Systems, 14(2):80-3.
- Sinha, R. and Boutelle, J. (2004). Rapid information architecture prototyping. In DIS ’04: Proceedings of the 2004 conference on Designing interactive systems, pages 34-352, New York, NY, USA. ACM Press.
- Smith, E. E. and Medin, D. L. (1981). Categories and Concepts. Harvard University Press, Cambridge, Massachusetts.
- Spencer, D. (2009). Card Sorting - Designing Usable Categories. Rosenfeld Media, Brooklyn, New York.
- Tullis, T. and Wood, L. (2004). How many users are enough for a card-sorting study? In Proceedings UPA’2004, Minneapolis, MN.
- Upchurch, L., Rugg, G., and Kitchenham, B. (2001). Using card sorts to elicit web page quality attributes. IEEE Software, 18(4):84-8.
- Uschold, M. and Gruninger, M. (1996). Ontologies: Principles, methods and applications. Knowledge Engineering Review, 11(2).
- Wittgenstein, L. (1953). Philosophische Untersuchungen. Blackwell, Oxford. English translation Philosophical Investigations; trans. and ed. by G.E.M. Anscombe; second edition 158.
- Wodtke, C. (2002). Information Architecture: Blueprints for the web. New Riders, Berkeley - CA - US.
- Xu, R. and Wunsch, D. (2005). Survey of clustering algorithms. Ieee Transactions On Neural Networks, 16(3):645-678.
Footnotes
[1]. Nowadays, at least three different families of theories try to explain how the categorization process works in our minds: the prototype theory (the categorization is based on the similarity of each element with a number of prototypes); the exemplar theory (which assumes that there are no such things like abstract prototypes, but just past encountered exemplars stored in memory) and the theory theory (which assumes that the process requires and is based upon some naive theories of the world); the most recent approaches assumes that people use, implicitly and unconsciously, all those strategies in different contexts (Ashby and Maddox, 2005). For the purposes of this article, however, we can refer to the classical work of Eleanor Rosch and her colleagues.
[2]. Unlike in a typical card sorting task, the correct answer is known by the experimenter, and therefore the answers of the participants can be judged as correct or wrong.
[3]. This dataset will be used for the case study in the following chapters.
[4]. The hierarchical cluster analysis, the so called htree, is the clustering technique most often used in the analysis of card sorting: see Coxon (1999), Faiks and Hyland (2000), Sinha and Boutelle (2004), and Tullis and Wood (2004).

